Unidad 1.

1. DATOS AGRUPADOS  Y NO AGRUPADOS

Datos Agrupados

Los datos agrupados son como lo indica su nombre, una cantidad dada de datos que puede clasificarse, ya sea por sus cualidades cualitativas o cuantitativas, y por tal agruparse para su análisis.

Los datos agrupados en frecuencia: son los que se distribuyen u organizan en una tabla de frecuencia (La frecuencia es igual al número de veces en que se repite cada valor en una serie de datos.), así, Por medio de ella, es fácil identificar la cantidad de respuestas repetidas.

Los datos agrupados por intervalos: son los que se organizan dentro de un rango y se delimita su amplitud por límites establecidos. Así, por medio de esta, es fácil identificar la cantidad de elementos en un determinado rango de valores.

1.- su fin es resumir la información mediante el uso de de tablas que organizan sus elementos y agrupan sus valores para ser presentados numérica o gráficamente. Esto implica: ordenar, clasificar y expresar los en una tabla de frecuencias o intervalos.

2.- Se agrupa a los datos, si se cuenta con 20 o más elementos. Aunque contemos con más de 20 elementos, debe de verificarse que los datos n sean significativos, esto es: que la información sea “repetitiva”, también debemos de verificar que los datos puedan clasificarse. Y que dicha clasificación tiene coherencia y lógica (de acuerdo a lo que se nos está pidiendo).

 Ejemplos:

Se busca determinar el número de niños en cada uno de los grados escolares de una primaria, (del 1 al 6 grado), por lo que se recolectan los datos y se organizan y agrupan en una tabla de frecuencias.

Edad..........Frecuencia
1..................2
2..................4
3..................7
4..................4
5..................2
6..................1
Total............20

Agrupación en intervalos, por ejemplo, de 2 años para este caso.

Edad..........Frecuencia
1-2...............6
3-4...............11
5-6...............3
Total.............20

DATOS NO AGRUPADOS

Los datos no agrupados son el conjunto de datos que no se ha clasificado y se es presentada en su forma de aparición en una tabla de datos donde cada valor se representa de forma individual. Por lo general este conjunto comprende una cantidad de elementos menor a 30 (n<30) con poca o nula repetición.

.

Ejemplo:

Vas a investigar la edad a un grupo de 20 Niños en datos no agrupados (es decir, vienen los 20 niños y así como te dan la edad así la anotas)

2,2,1,3,3,3,4,4,5,6,1,2,2,3,3,3,4,4,3,6 (Total 20 niños)

Estos son datos no agrupados por qué no los has clasificado y contado.1,1,2,2,2,2,3,3,3,3,3,3,3,4,4,4,4,5,5,6 (Total 20 niños)

Los datos no agrupados también los puedes ordenar, por ejemplo de la edad menor a la edad mayor, no están contabilizados ni clasificados solamente están ordenados.

En una investigación sobre el calentamiento de varios elementos líquidos para determinar en cada uno de ellos el punto, la temperatura, en la cual cambian de estado, los científicos van anotando las temperaturas que van dando efecto.

134°C, 345°C, 234°C, 456°C, 837°C, 456°C, 122°C, 4567°C, 3456°C, 456°C, 190°C,  900°C.

estas medidas pueden ser apiladas en una tabla de datos, y mantener su independencia como valor unico y representativo

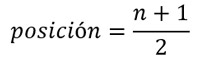
2.  CUARTILES

Los cuartiles son los tres valores de la variable que dividen a un conjunto de datos ordenados en cuatro partes iguales.

Q₁, Q₂ y Q₃ determinan los valores correspondientes al 25%, al 50% y al 75% de los datos.Q₂ coincide con la mediana.

Cálculo de los cuartiles
1 Ordenamos los datos de menor a mayor.2 Buscamos el lugar que ocupa cada cuartil mediante la expresión .Número impar de datos
2, 5, 3, 6, 7, 4, 9

Número par de datos
2, 5, 3, 4, 6, 7, 1, 9

Cálculo de los cuartiles para datos agrupados
En primer lugar buscamos la clase donde se encuentra , en la tabla de las frecuencias acumuladas.
Ejercicio de cuartiles
Calcular los cuartiles de la distribución de la tabla

	fi	Fi
[50, 60)	8	8
[60, 70)	10	18
[70, 80)	16	34
[80, 90)	14	48
[90, 100)	10	58
[100, 110)	5	63
[110, 120)	2	65
	65

Cálculo del primer cuartil

Cálculo del segundo cuartil

Cálculo del tercer cuartil

2 . Deciles

Los deciles son los nueve valores que dividen la serie de datos en diez partes iguales.
Los deciles dan los valores correspondientes al 10%, al 20%... y al 90% de los datos.D₅ coincide con la mediana.

Cálculo de los decilesEn primer lugar buscamos la clase donde se encuentra , en la tabla de las frecuencias acumuladas.
Ejercicio de deciles

Calcular los deciles de la distribución de la tabla:

	fi	Fi
[50, 60)	8	8
[60, 70)	10	18
[70, 80)	16	34
[80, 90)	14	48
[90, 100)	10	58
[100, 110)	5	63
[110, 120)	2	65
	65

Cálculo del primer decil

Cálculo del segundo decil

4. TABLA DE DISTRIBUCIÓN DE FRECUENCIA

Qué es una tabla de frecuencias

La tabla de frecuencias es una tabla donde los datos estadísticos aparecen bien organizados, distribuidos según su frecuencia, es decir, según las veces que se repite en la muestra.En esta tabla se representan los diferentes tipos de frecuencias, ordenados en columnas.La tabla de frecuencias es una herramienta que permite la realización de los gráficos o diagramas estadísticos de una forma más fácil.

Cómo construir una tabla de frecuencias con datos agrupados en intervalos. Ejemplo resuelto.

Si tenemos un número muy grande de datos, éstos se agrupan en intervalos, para no tener que realizar tablas muy largas con muchos datos diferentes. También se agrupan en intervalos cuando las variables son continuas.

En estos caso se realiza una tabla de frecuencias con datos agrupados.

Los datos se agrupan en intervalos, llamados clases y es a estos intervalos  los que se asignan sus frecuencias correspondientes.

Sobre las clases, debes conocer los siguientes conceptos:

• Límites de clase: Cada intervalo tiene un límite inferior, que pertenece a ese intervalo (cerrado por la izquierda con un corchete) y un límite superior que no pertenece (abierto por la derecha)
• Amplitud de clase: La amplitud es la diferencia entre el límite superior e inferior y debe ser la misma para cada intervalo
• Marca de clase: Es el punto medio de cada intervalo y es el valor que se utiliza para calcular otras medidas (realmente para el cálculo de frecuencias no es necesario este valor)

Vamos a ver un ejemplo de realizar una tabla de frecuencias con datos agrupados en intervalos:

Se toma una muestra de peces de una cierta especie y se miden sus longitudes en centímetros, cuyos resultados son:

Obtener la tabla de frecuencias absolutas, relativas y acumuladas.

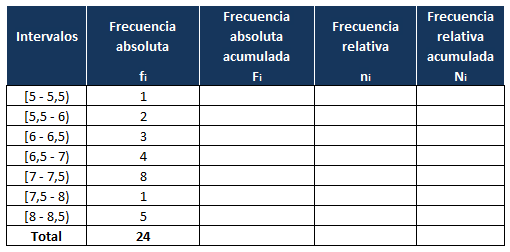
La tabla de frecuencias tendrá las siguientes 5 columnas:

• Intervalos
• Frecuencia absoluta (fi)
• Frecuencia absoluta acumulada (Fi)
• Frecuencia relativa (ni)
• Frecuencia relativa acumulada (Ni)

Para rellenar la primera columna, tenemos que determinar el número de intervalos y la amplitud de los mismos. Para ello se identifica el valor más pequeño y el valor más grande, que en este caso son 5,42 y 8,42 respectivamente.

Ahora concretamos el número de intervalos que queremos y la amplitud para cada intervalo. Podemos hacerlo por ejemplo que con una amplitud de 0,5 y que empiecen desde 5 y lleguen hasta 8,5.

Nos quedan los siguientes intervalos:

Dejamos la última fila para el total.

Si queremos tener menos intervalos, sólo tenemos que ampliar la amplitud.

Para completar la columna de frecuencia absoluta, tenemos que ir contando los valores que pertenecen a cada intervalo.

Si por ejemplo tuviéramos el valor 5,5,  pertenecería al segundo intervalo y no al primero, ya que el primer intervalo es abierto hasta 5,5, es decir, el 5,5 no está incluido y el segundo intervalo comienza a partir de 5,5, que sí está incluido, ya que el intervalo es cerrado por la izquierda.

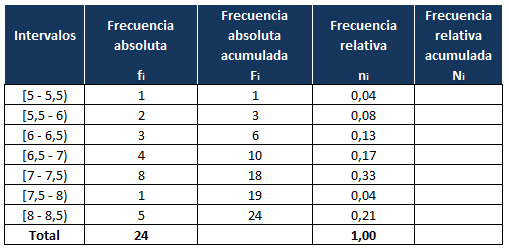
Después de contar nos queda de la siguiente manera:

Para completar la columna de la frecuencia absoluta acumulada de cada intervalo lo hacemos igual que en el caso anterior:en la primera fila, la frecuencia absoluta acumulada coincide con la frecuencia absoluta y para el resto de filas, la frecuencia absoluta acumulada la obtenemos sumando la frecuencia absoluta acumulada del dato anterior (del dato de arriba) más su frecuencia acumulada (dato de su izquierda).

Nos queda:

La frecuencia relativa la calculamos dividiendo cada frecuencia absoluta, entre el número total de elementos:

Por ejemplo, para el tercer intervalo, la frecuencia relativa es:

Lo hacemos igual para el resto de intervalos y en la última fila, colocamos la suma de las frecuencias relativas:

La frecuencia relativa acumulada del primer dato es igual que su frecuencia relativa y para los datos siguientes es igual a su frecuencia relativa más la frecuencia relativa del dato anterior (del dato de arriba):

O bien la podemos calcular la frecuencia relativa acumulada, dividiendo cada frecuencia absoluta acumulada entre el número de elementos total:

Media

La media se calcula usando la siguiente fórmula:

Ejemplo 1

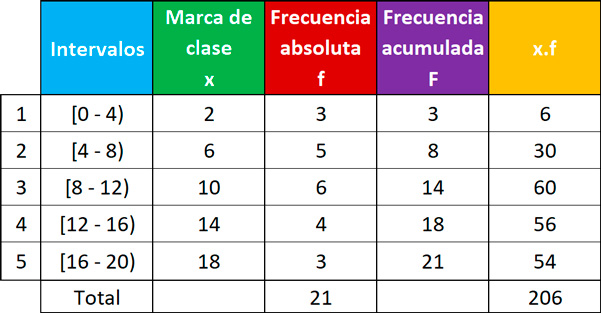
Determina la media de la siguiente distribución:

Dado que tenemos 5 intervalos, la media la calculamos usando la fórmula:

En la tabla, agregamos una columna donde colocaremos todos los valores de x.f :

Calculamos los valores de x.f :

Finalmente, calculamos el valor de la media, dividiendo la suma de valores de la columna x.f entre n.

El valor de la media sería 39,238.

Mediana

Para estimar la mediana, hay que seguir 2 pasos:

• Encontrar el intervalo en el que se encuentra la mediana usando la fórmula:

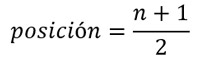
• Usar la fórmula de la mediana:

Donde:

• Li: límite inferior del intervalo en el cual se encuentra la mediana.
• n: número de datos del estudio. Es la sumatoria de las frecuencias absolutas.
• Fi-1: frecuencia acumulada del intervalo anterior al que se encuentra la mediana.
• Ai: amplitud del intervalo en el que se encuentra la mediana.
• fi: frecuencia absoluta del intervalo en el que se encuentra la mediana.

Ejemplo 2

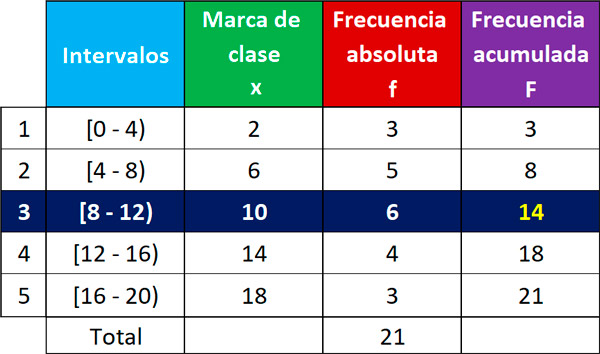
Encontrar la mediana de la siguiente distribución:

Para estimar el valor de la mediana, seguimos los 2 pasos.

Primero encontramos el intervalo en el cual se encuentra la mediana usando la fórmula:

Este valor, lo buscamos en la columna de frecuencias acumuladas. Si no aparece, buscamos el valor que sigue. Como vemos, después del 11 sigue el 14, por lo tanto, la mediana se ubica en el intervalo 3.

Ahora, aplicamos la fórmula de la mediana:

El valor de la mediana, sería:  Me = 9,667.

Moda

Para estimar la moda, se siguen los siguientes pasos:

• Encontrar el intervalo en el cual se encuentra la moda, que es el intervalo con mayor frecuencia absoluta.
• Usar la siguiente fórmula para estimar el valor de la moda:

Donde:

• Li: límite inferior del intervalo en el cual se encuentra la moda.
• fi-1: frecuencia absoluta del intervalo anterior en el que se encuentra la moda.
• fi: frecuencia absoluta del intervalo en el que se encuentra la moda.
• fi+1: frecuencia absoluta del intervalo siguiente en el que se encuentra la moda.
• Ai: amplitud del intervalo en el que se encuentra la moda.

EJERCICIOS REALIZADOS EN CLASE:

VIDEO EXPLICACIÓN:

https://www.youtube.com/watch?v=lZOleQMMp4U

5. GRÁFICOS

DIAGRAMA DE BARRASEs una forma gráfica de representar datos cualitativos que se han resumido en una distribución de frecuencias, de relativas o de porcentuales. Hay varios tipos de gráficos de barras, como son :

DIAGRAMA CIRCULAR  
Es de especial utilidad para mostrar proporciones ( porcentajes ) relativas de una variable. Se crea marcando una porción del círculo correspondiente a cada categoría de la variable . 




GRÁFICAS  DE LINEA Se ilustra  mediante segmentos de línea los cambios en cantidades con respecto al tiempo. Son especialmente útiles en el comercio y en los negocios.  




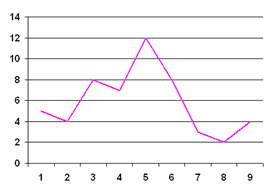
HISTOGRAMAS Una de las maneras más comunes de representar una distribución de frecuencia . Su grafica consiste en un conjunto de barras, en la que la base de cada barra representa una clase o intervalo, indicada en el eje horizontal,  y la altura por su frecuencia, indicada en el eje vertical. Generalmente las barras se trazan adyacentes una a la otra. 






OJIVA Es un polígono acumulado de frecuencia absoluta ,relativa o porcentual  y por lo tanto representa segmentos de línea  que se origina al conectar los puntos formados por la intersección entre el límite inferior de cada clase con la frecuencia acumulada. Es conocida como  POLÍGONO DE FRECUENCIA ACUMULADA MENOR QUE  , ya que muestra el número o porcentaje de observaciones menores a cierto valor. La  ojiva es importante por que nos permite extrapolar información que la distribución de frecuencia oculta y así como calcular estadísticos como la mediana, cuartiles, deciles y percentiles, en forma aproximada. Para construir la ojiva se debe primero elaborar la distribución de frecuencia menor que.